Problems in Estimating Sample Size for Hypothesis Testing

In the module on hypothesis testing for means and proportions, we introduced techniques for means, proportions, differences in means, and differences in proportions. While each test involved details that were specific to the outcome of interest (e.thou., continuous or dichotomous) and to the number of comparison groups (ane, two, more than two), there were common elements to each test. For case, in each exam of hypothesis, at that place are two errors that can exist committed. The offset is called a Blazon I error and refers to the situation where we incorrectly reject H0 when in fact it is truthful.   In the commencement pace of any test of hypothesis, we select a level of significance, α , and α = P(Blazon I error) = P(Reject H0 | H0 is true). Because we purposely select a small value for α , we command the probability of committing a Type I error. The 2d blazon of error is chosen a Type Two error and it is defined as the probability nosotros do not decline H0 when information technology is simulated. The probability of a Type II error is denoted β , and β =P(Blazon 2 error) = P(Practice non Reject H0 | H0 is simulated). In hypothesis testing, we usually focus on ability, which is defined as the probability that we refuse H0 when it is false, i.e., power = 1- β = P(Reject H0 | H0 is false). Ability is the probability that a exam correctly rejects a false zilch hypothesis. A good examination is one with low probability of committing a Type I error (i.e., minor α ) and high power (i.e., small β, high power).

Here nosotros nowadays formulas to decide the sample size required to ensure that a exam has high ability. The sample size computations depend on the level of significance, aα, the desired ability of the test (equivalent to i-β), the variability of the outcome, and the effect size. The effect size is the departure in the parameter of interest that represents a clinically meaningful divergence. Like to the margin of mistake in confidence interval applications, the issue size is determined based on clinical or practical criteria and non statistical criteria.

The concept of statistical ability tin can be difficult to grasp. Before presenting the formulas to make up one's mind the sample sizes required to ensure high power in a examination, we will offset discuss power from a conceptual point of view.

Suppose we want to test the following hypotheses at aα=0.05:  H0: μ = 90 versus H1: μ ≠ ninety. To test the hypotheses, suppose we select a sample of size northward=100. For this instance, assume that the standard departure of the consequence is σ=20. We compute the sample mean and then must decide whether the sample mean provides bear witness to support the culling hypothesis or not. This is done by computing a test statistic and comparing the test statistic to an appropriate disquisitional value. If the nothing hypothesis is truthful (μ=90), then we are likely to select a sample whose mean is shut in value to 90. However, it is besides possible to select a sample whose mean is much larger or much smaller than 90. Recall from the Primal Limit Theorem (encounter folio 11 in the module on Probability), that for large n (here n=100 is sufficiently big), the distribution of the sample means is approximately normal with a mean of

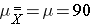
and

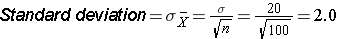
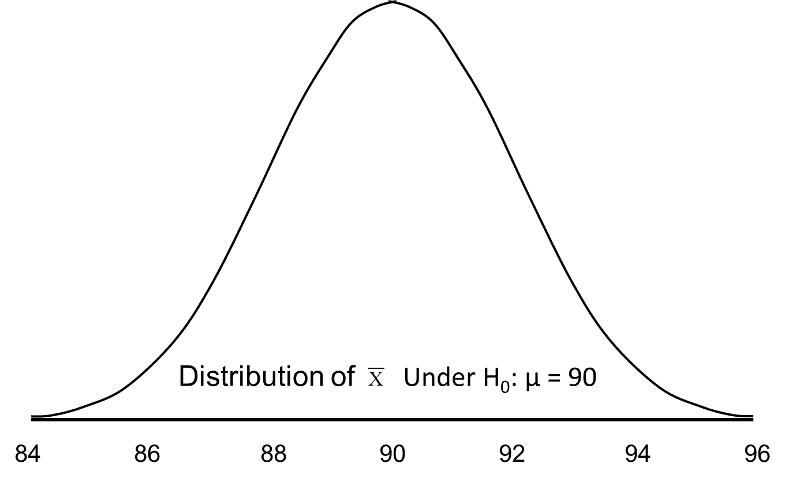
If the null hypothesis is true, it is possible to observe any sample mean shown in the figure beneath; all are possible under H0: μ = 90.

Normal distribution of X when the mean of X is 90. A bell-shaped curve with a value of X-90 at the center.

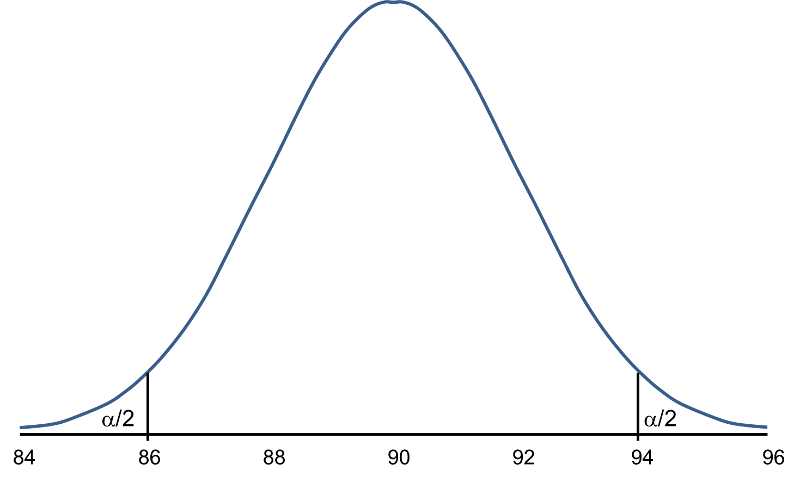
When nosotros set up the decision rule for our exam of hypothesis, we decide disquisitional values based on α=0.05 and a ii-sided test. When we run tests of hypotheses, nosotros usually standardize the data (e.g., convert to Z or t) and the disquisitional values are advisable values from the probability distribution used in the test. To facilitate interpretation, we will continue this give-and-take with x-bar.png as opposed to Z. The critical values for a two-sided test with α=0.05 are 86.06 and 93.92 (these values correspond to -1.96 and i.96, respectively, on the Z calibration), so the decision rule is every bit follows: Reject H0 if x-bar.png < 86.06 or if x-bar.png > 93.92. The rejection region is shown in the tails of the figure beneath.

Rejection Region for Test H0: μ = ninety versus Hi: μ ≠ 90 at α =0.05

Standard normal distribution showing a mean of 90. The rejection areas are in the two tails at the extremes above and below the mean. If the alpha level is 0.05, then each tail accounts for an arean of 0.025. .

The areas in the ii tails of the curve represent the probability of a Blazon I Error, α= 0.05. This concept was discussed in the module on Hypothesis Testing.

Now, suppose that the alternative hypothesis, Hi, is truthful (i.eastward., μ ≠ xc) and that the true hateful is really 94. The effigy below shows the distributions of the sample mean under the null and alternative hypotheses.The values of the sample mean are shown along the horizontal axis.

Distribution of 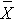Under H0: μ = ninety and Under Hane: μ = 94

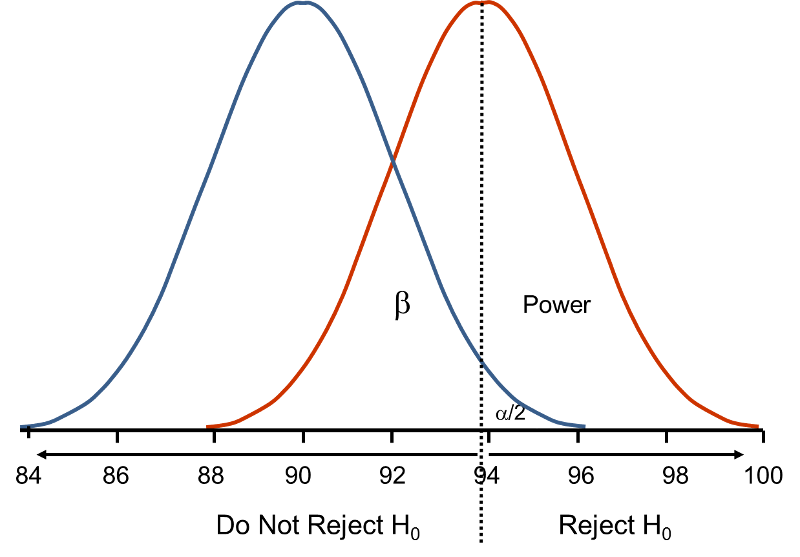
Two overlapping normal distributions, one depicting the null hypothesis with a mean of 90 and the other showing the alternative hypothesis with a mean of 94. A more complete explanation of the figure is provided in the text below the figure.

If the truthful mean is 94, then the culling hypothesis is true. In our test, we selected α = 0.05 and reject H0 if the observed sample hateful exceeds 93.92 (focusing on the upper tail of the rejection region for now). The disquisitional value (93.92) is indicated by the vertical line. The probability of a Blazon II mistake is denoted β, and β = P(Practice not Reject H0 | H0 is faux), i.e., the probability of not rejecting the cipher hypothesis if the nada hypothesis were true. β is shown in the effigy above as the surface area under the rightmost curve (H1) to the left of the vertical line (where we do not reject H0). Power is defined as 1- β = P(Pass up H0 | H0 is false) and is shown in the figure as the surface area under the rightmost curve (Hane) to the right of the vertical line (where nosotros refuse H0 ).

Annotation that β and power are related to α, the variability of the outcome and the effect size. From the effigy above we can meet what happens to β and power if we increase α. Suppose, for case, we increase α to α=0.10.The upper critical value would be 92.56 instead of 93.92. The vertical line would shift to the left, increasing α, decreasing β and increasing power. While a better test is one with college power, it is not advisable to increase α as a means to increase power. Nonetheless, there is a direct relationship between α and power (as α increases, and so does power).

β and power are also related to the variability of the result and to the effect size. The issue size is the difference in the parameter of interest (e.chiliad., μ) that represents a clinically meaningful divergence. The figure higher up graphically displays α, β, and power when the difference in the mean under the null as compared to the alternative hypothesis is 4 units (i.east., ninety versus 94). The figure below shows the same components for the state of affairs where the hateful under the culling hypothesis is 98.

Figure - Distribution of  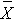 Nether H0: μ = 90 and Nether H1: μ = 98.

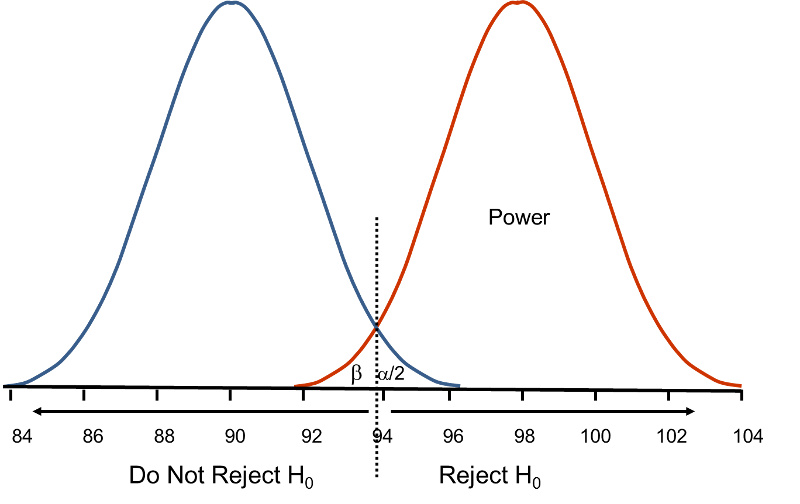
Overlapping bell-shaped distributions - one with a mean of 90 and the other with a mean of 98

Notice that there is much college ability when there is a larger divergence between the mean under H0 as compared to H1 (i.e., ninety versus 98). A statistical test is much more likely to decline the null hypothesis in favor of the alternative if the true mean is 98 than if the true hateful is 94. Notice also in this instance that in that location is piddling overlap in the distributions under the zero and alternative hypotheses. If a sample mean of 97 or college is observed it is very unlikely that it came from a distribution whose mean is ninety. In the previous effigy for H0: μ = xc and H1: μ = 94, if we observed a sample mean of 93, for example, it would not be equally clear every bit to whether it came from a distribution whose hateful is 90 or one whose mean is 94.

Ensuring That a Test Has Loftier Power

In designing studies most people consider power of 80% or 90% (just every bit we mostly apply 95% every bit the conviction level for confidence interval estimates). The inputs for the sample size formulas include the desired power, the level of significance and the outcome size. The effect size is selected to stand for a clinically meaningful or practically of import departure in the parameter of involvement, as we volition illustrate.

The formulas we present below produce the minimum sample size to ensure that the test of hypothesis will have a specified probability of rejecting the null hypothesis when it is simulated (i.e., a specified power). In planning studies, investigators once more must account for attrition or loss to follow-up. The formulas shown beneath produce the number of participants needed with complete information, and we will illustrate how attrition is addressed in planning studies.

return to meridian | previous page | next folio